
Un filo inestendibile è legato a due punti fissi del piano.

Ellissografo ad antiparallelogramma
In un antiparallelogramma articolato uno dei due lati minori è fissato a un piano. Il tracciatore si trova nel punto di intersezione di due lati.

Guida rettilinea di Kempe a rombo articolato
Un rombo articolato ABCD ha un lato AB imperniato al piano. Ai vertici A e C sono collegate due aste di uguale lunghezza incernierate in G, a cui è vincolata una terza asta, di lunghezza uguale a GA, collegata al punto E del lato DC.

È composto da due aste incernierate tramite un ingranaggio; una delle due aste si può allungare.

Sull’intersezione fra due lati consecutivi e una retta parallela alla diagonale di un rombo articolato sono fissati due cursori che possono scorrere in una scanalatura. Un vertice descrive una circonferenza il vertice opposto una ellisse.

Due parallelogrammi sono articolati con un lato in comune; l’altro lato di uno dei due parallelogrammi è fissato al piano del modello.

In un perno fisso può scorrere l’asta di un sistema di due aste ortogonali. Il perno nell’angolo retto può scorrere nell’asta di un altro sistema di due aste ortogonali, avente l’altra asta scorrevole in una scanalatura passante per il perno fisso.

Un’asta può scorrere in una scanalatura mantenendosi durante il movimento perpendicolare ad essa. Un filo inestendibile ha un estremo fissato alla sommità dell’asta e l’altro in un punto del piano.

Uno dei problemi che ha impegnato gli ingegneri negli anni a cavallo tra il XVIII e il XIX secolo è stato quello di trovare un sistema utile per guidare l’asta del pistone di una macchina a vapore in un moto rettilineo alternato.

La lemniscata fu descritta nel 1694 da Jakob Bernoulli, come variante dell’ellisse. Bernoulli la chiamò lemniscus, derivante dal greco λημνίσκος, lemníscos, equivalente latino di fiocco pendente. La curva era già stata trattata da Giovanni Cassini nel suo studio del 1680 sull’ovale di Cassini, di cui costituisce un caso particolare.

Iperbolografo di Delaunay
Iperbolografo a rombo articolato.

Ellissografo di Proclo

Parabola per inviluppo

Iperbolografo ad antiparalellogramma

Conicografo a filo

Concoide di Dürer

Lumache di Pascal

Concoide di Nicomede
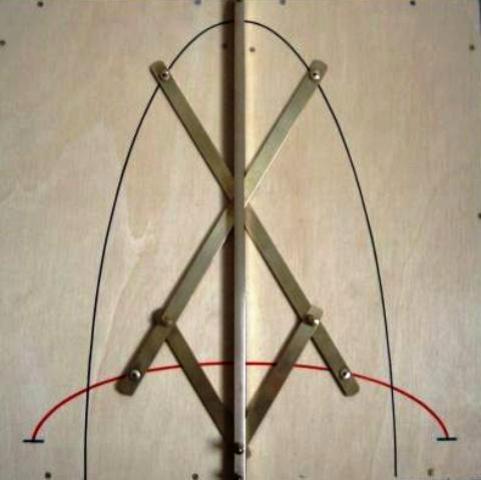
Ellissografo di Leonardo

Sfera di Lénárt
La geometria sferica con la Sfera di Lénárt